第一单元 | Ascendira

题意简述

形式化表达

表达式 → 空白项 [加减空白项] 项空白项 | 表达式加减空白项项空白项
项 → [加减空白项] 因子 | 项空白项 ‘*’ 空白项因子
因子 → 变量因子 | 常数因子 | 表达式因子｜求导因子
变量因子 → 幂函数 | 指数函数 | 自定义函数调用
常数因子 → 带符号的整数
表达式因子 → ‘(‘ 表达式 ‘)’ [空白项指数]
幂函数 → 自变量 [空白项指数]
自变量 → ‘x’
指数函数 → ‘exp’ 空白项 ‘(‘ 空白项因子空白项 ‘)’ [空白项指数]
指数 → ‘^’ 空白项 [‘+’] 允许前导零的整数 (注：指数一定不是负数)
带符号的整数 → [加减] 允许前导零的整数
允许前导零的整数 → (‘0’|’1’|’2’|…|’9’){‘0’|’1’|’2’|…|’9’}
空白项 → {空白字符}
空白字符 → （空格） | \t
加减 → ‘+’ | ‘-‘

自定义函数相关(相关限制见“公测数据限制”)

自定义函数定义 → 自定义函数名空白项 ‘(‘ 空白项形参自变量空白项 [‘,’ 空白项形参自变量空白项 [‘,’ 空白项形参自变量空白项]] ‘)’ 空白项 ‘=’ 空白项函数表达式
形参自变量 → ‘x’ | ‘y’ | ‘z’
自定义函数调用 → 自定义函数名空白项 ‘(‘ 空白项因子空白项 [‘,’ 空白项因子空白项 [‘,’ 空白项因子空白项]] ‘)’
自定义函数名 → ‘f’ | ‘g’ | ‘h’
函数表达式 → 表达式（将自变量扩展为形参自变量，且一定不含求导因子） (注：本次作业函数表达式中可以调用其他自定义函数，但保证不会出现递归调用的情况)

求导算子相关(相关限制见“公测数据限制”)

求导因子 → 求导算子空白项 ‘(‘ 空白项求导因子空白项 ‘)’ | 求导算子空白项 ‘(‘ 空白项表达式空白项 ‘)’
求导算子 → ‘dx’

要求

输入格式
输出格式
数据限制
判定模式
正确性判定
性能判定

一、程序架构分析

1. 类图分析

最终架构总UML图

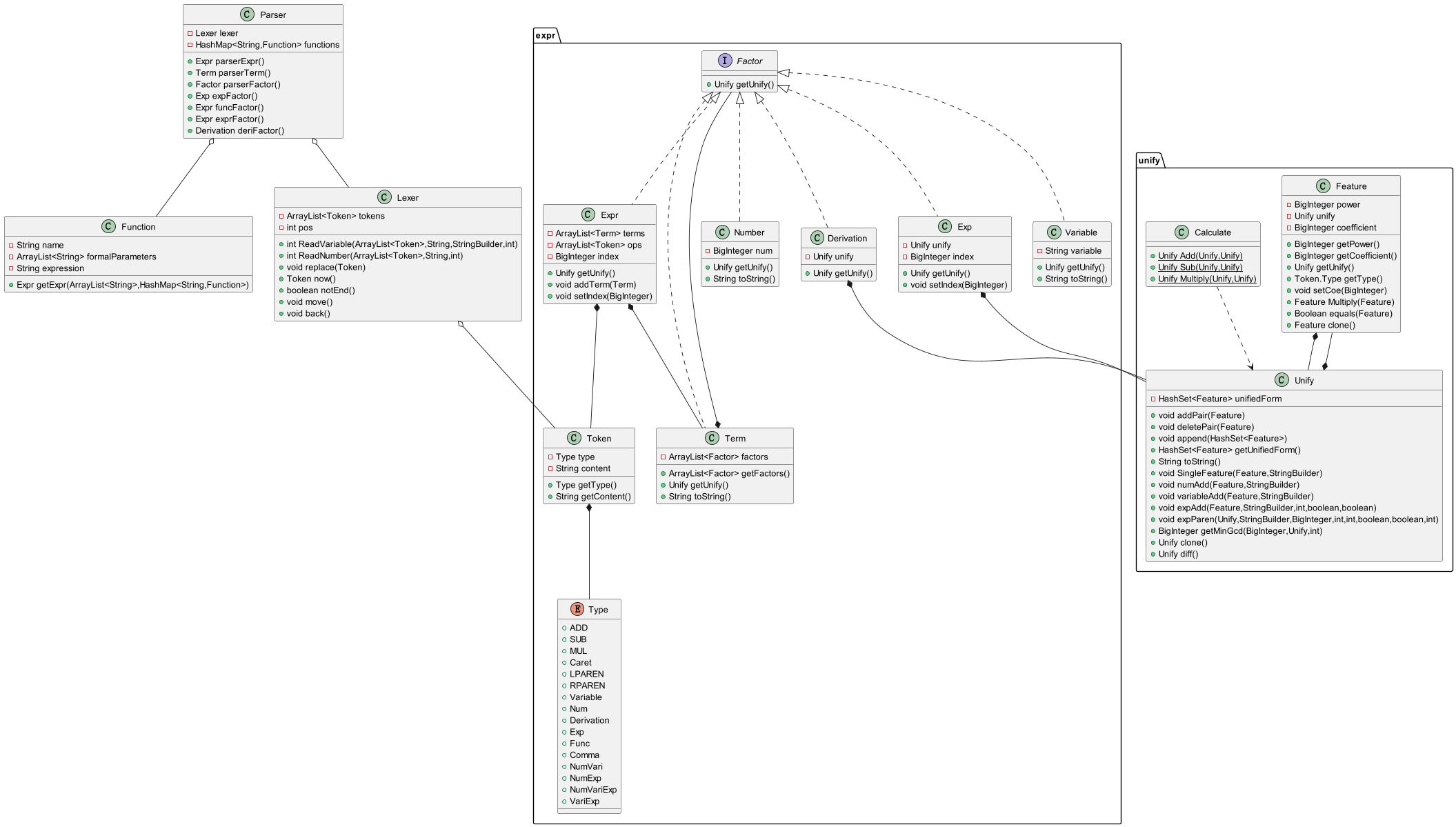
unit_1

最终架构由三个部分组成，表达式构造部分，表达式预处理部分，表达式化简与输出部分，各部分间赋予相应的功能，最终完成本单元任务。

表达式化简与输出部分

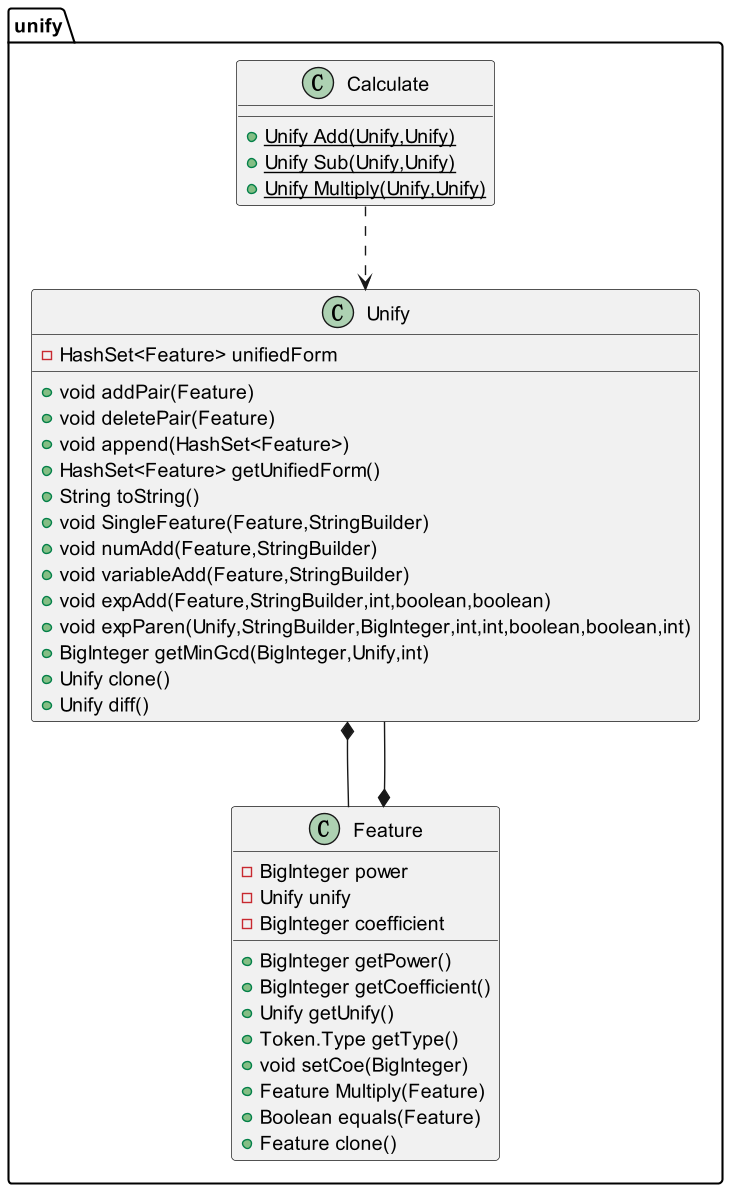
unify

表达式化简

我使用类Unify来表示每个Factor的最简形式，启发来自于每个Factor均由$ ka^mexp^{factor}$表示或者组成，故使用类Feature表示$ ka^mexp^{factor}$，Feature的power,unify,coefficient分别表示m,factror,k。使用HashSet来存放每个Factor的最简形式——Feature//单项式或者HashSet<Feature>//多项式，故HashSet<Feadture>是Unify的主体部分（使用HashSet的原因是其本身所具有的互异性体现了表达式化简的过程）。

表达式输出

使用层次化方式，重写toString方法，调用方法SingleFeature完成Feature的输出，同时加上正负号。

由于每个Feature均由num,variable,exp构成，SingleFeature调用numAdd,variableAdd,expAdd完成输出。

处理两个Unify间的算法运算调用类Calculate的静态加法方法，静态减法方法，静态乘法方法完成，考虑到完成算法运算后得到的对象引用不能使用或者存在已有对象的引用，故需要调用类Unify的Unify clone()方法。

表达式优化

在进行表达式输出时完成，具体细节在优化策略中介绍。

表达式构造部分

expr

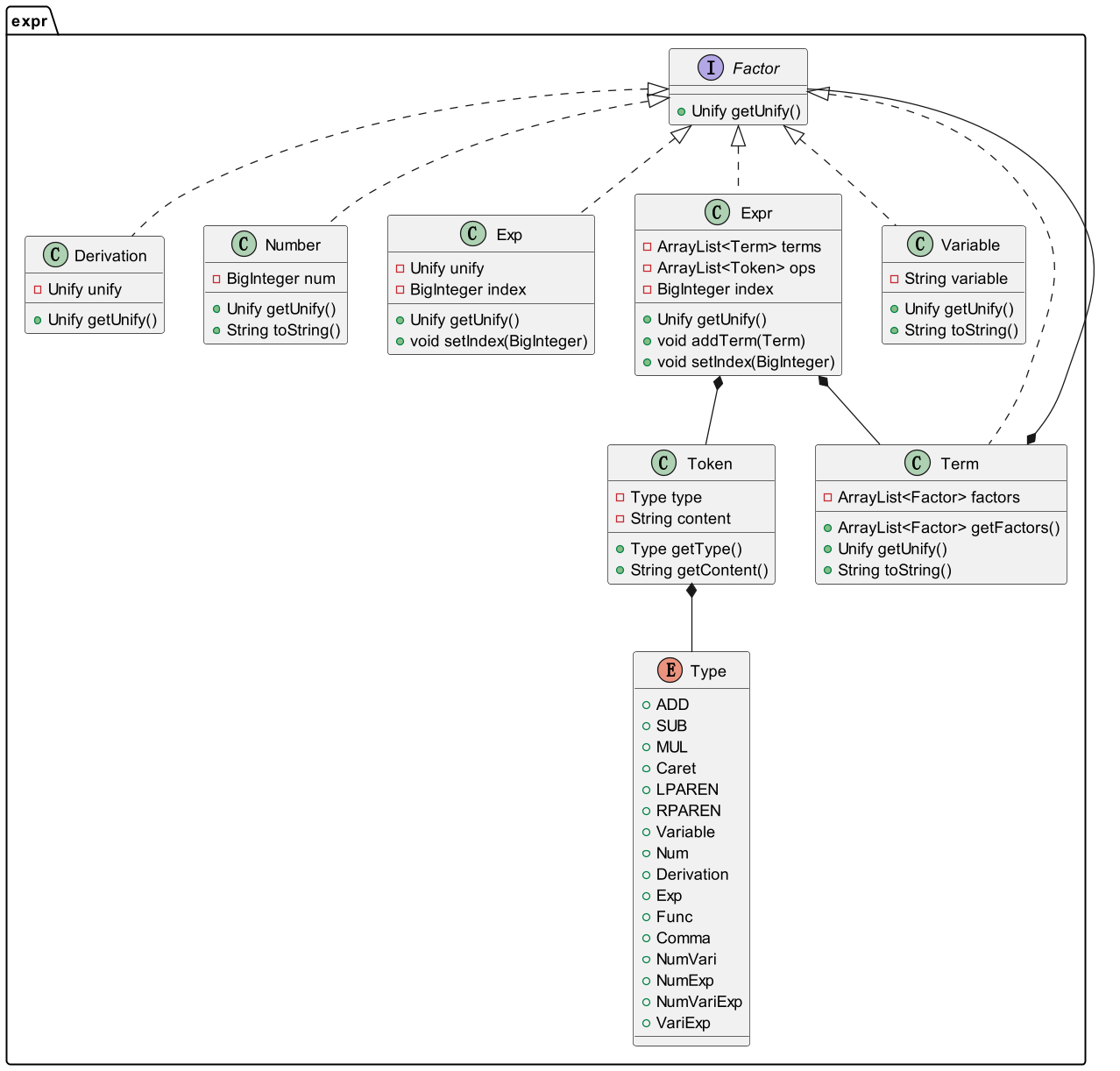
构成简述

表达式Expr由ArrayList terms（项），ArrayList ops（符号）以及index（指数）构成，Token组成上述ops。

项Term由ArrayList factors（因子）组成。

指数函数Exp使用对象Unify存放指数表达式，index表示指数。

导数Derivation使用对象Unify存放需进行求导的函数。

Derivation,Number,Exp,Expr,Variable,Term均实现接口Factor，均实现Unify getUnify()方法，从而得到每个Factor的最简形式。

表达式预处理部分

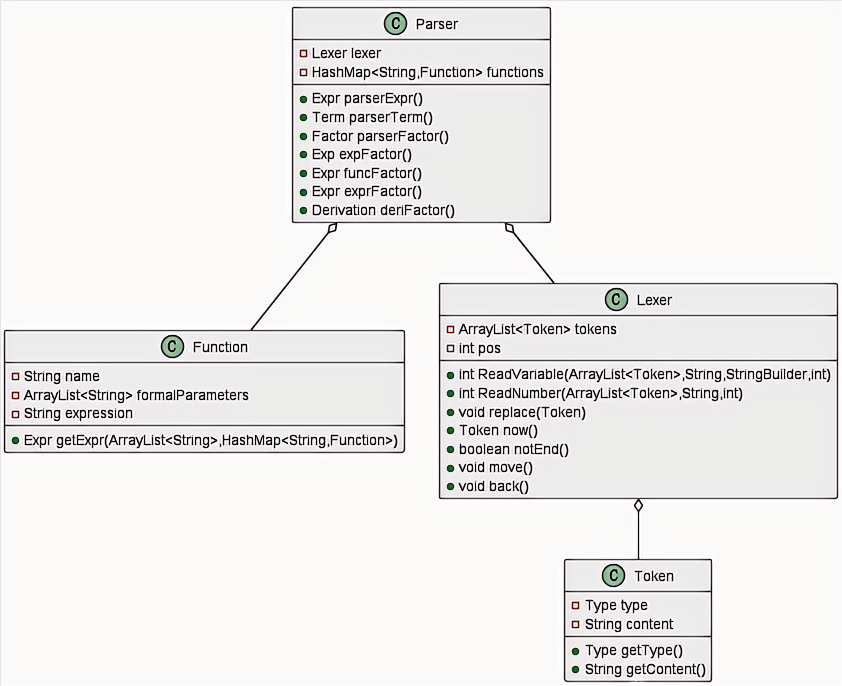
exprGen

过程简述

在MainClass中，根据输入格式，先读取自定义函数存入HashMap <String, Function>，key为自定义函数名，value为对象Function，类Function实现自定义函数定义，name,ArrayList <String> formalParameters,expression分别表示自定义函数名，形参自变量，函数表达式；再读取需要化简与输出的表达式，新建对象Lexer进行处理，pos记录当前字符位置，ArrayList<Token> tokens表示表达式中的所有符号;最后新建对象Paser，将functions和Lexer传入其中，使用递归下降法得到对象expr

子过程解析

Function

ArrayList <String> formalParameters不仅仅包含形参自变量的名称，还表示形参自变量的位置信息，这在Parser处理自定义函数的字符串时尤为关键。

Parser在遇到自定义函数时需调用该相应自定义函数对象（同名）的Expr getExpr(ArrayList<String> arguFactors, HashMap<String, Function> functions)方法，我的实现方法为字符串替换，新建对象StringBuilder，对expression进行遍历添加到上述对象中，遇到形参则将实参加入其中。

Lexer

完成对表达式中每个符号进行解析，具体分类参考Token.Type。
1
2
3
4
public enum Type {
        ADD, SUB, MUL, Caret, LPAREN, RPAREN, Variable, Num, Derivation,
        Exp, Func, Comma
    }
这里仅仅对Type.Variable，Type.Number进行特殊处理，Variable存入完整的幂函数（底数与指数），Number仅第一项只存入正数。

对于项与项之间的正负号直接抵消处理

Parser

利用递归下降的方法处理Lexer解析完成的表达式，首先调用Expr parserExpr()，其次再调用Term parserTerm()，然后再调用Factor parserFactor(),这时由于Factor可能是expr，exp再递归调用Expr parserExpr()，直至最后一层仅含Factor，除此之外，可能出现自定义函数，调用类Function进行处理；导数，调用类Derivation进行处理。

对于expr，exp，func，derivation均需调用其相应XXXXFactor方法，从而返回相应对象。

优缺点分析

优点

在该架构下，分别由三个部分完成相应的功能，整体架构较为明确，能较为容易完成迭代开发以及寻找bug。

充分利用递归下降法以及层次化遍历，完成对表达式的充分解析并能较好满足新元素融入后的调整迭代。

利用类Unify完成对所有Factor的统一表示，便于表达式化简的处理与输出优化。

缺点

Unify由于可完成对所有Factor的统一表示，故几乎再所有类中均有使用，并且其需要完成繁琐的化简输出，导致其由较高的复杂度。

2. 度量分析

代码规模

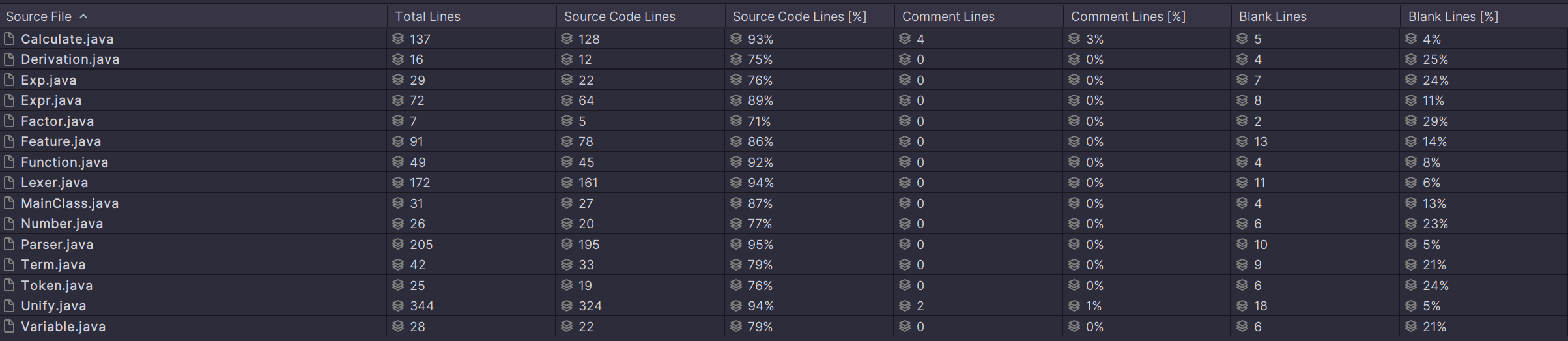
类复杂度
- 表达式构造部分
  
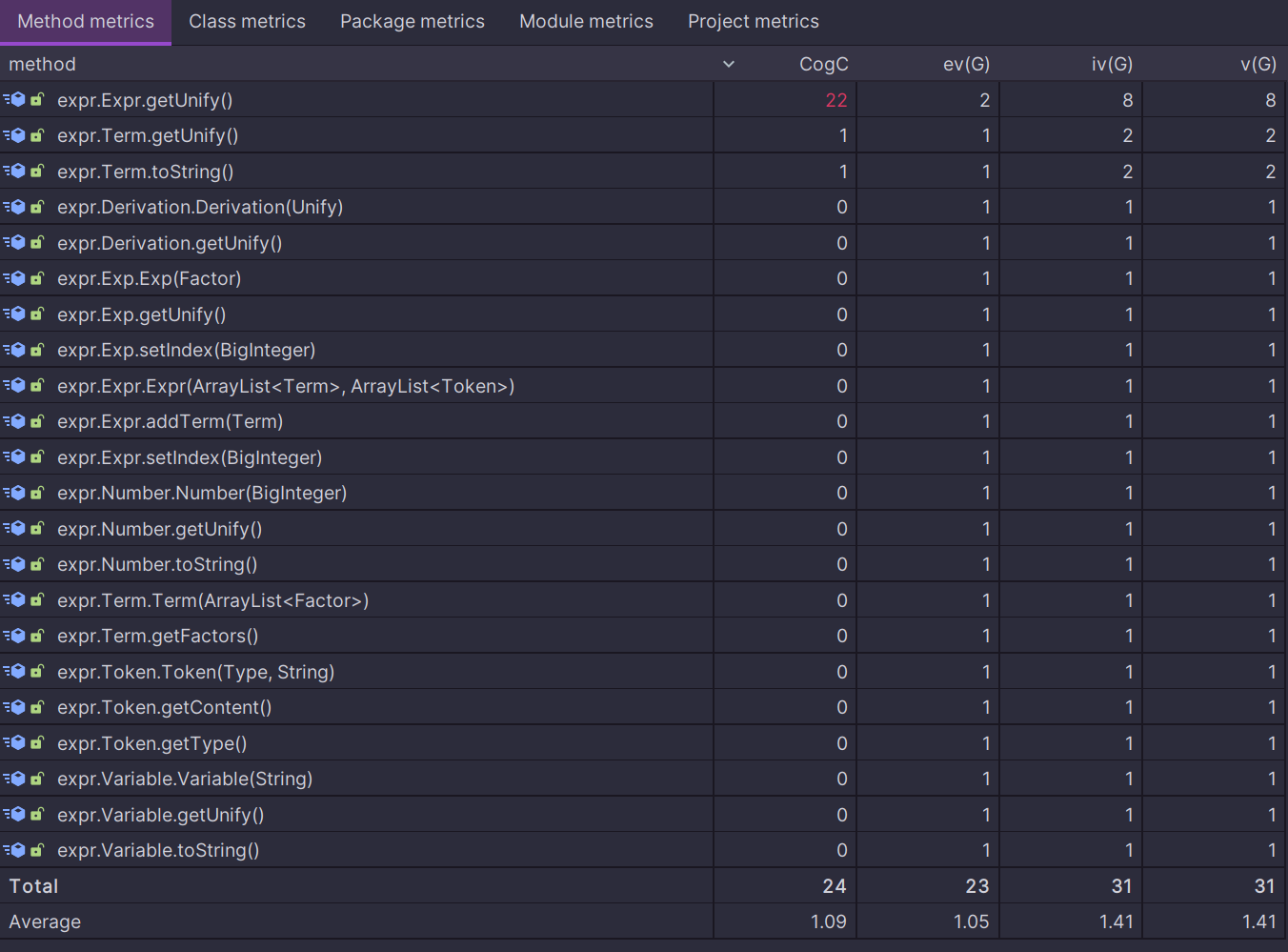
  expr的方法Unify getUnify()圈复杂度较高，由于其需完成项的遍历，项之间的加减运算，以及将项的乘积的转化为Feature，才能得到expr的unify，程序的整体控制流程较为复杂，但是在具体实现过程中需要调用类Calculate的静态方法，遍历与运算时分离的，具有较低的耦合度。
- 表达式预处理部分
  
  Parser的parseExpr()方法由于需要考虑第一项前符号问题，需进行分类讨论，故具有较高的复杂度。
  
  对于Lexer的ReadVariable(ArrayList<Token> tokens, String input, StringBuilder sb, int pos)和ReadNumber(ArrayList<Token> tokens, String input, int pos)方法，两者均需要考虑数字的前导0以及正负号问题，故具有较高的复杂度。
  
  Lexer的Lexer(String input)需要考虑各种符号的特殊情况，有较高的耦合度和复杂度。
- 表达式化简与输出部分
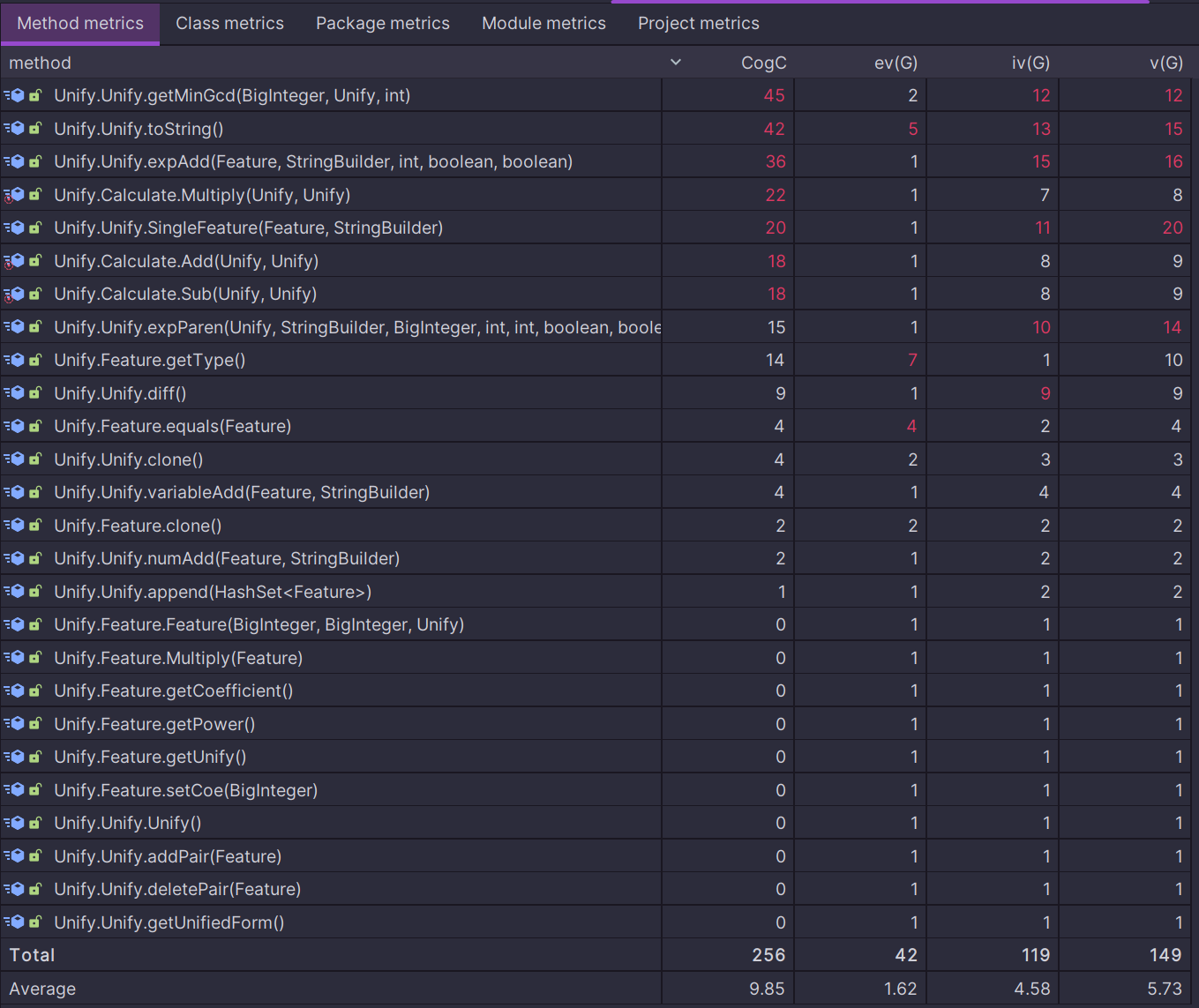
  - 在整个程序中，Unify的getMinGcd(BigInteger gcd, Unify unify, int initLength)有着最高的复杂度，这与表达式的输出优化有着巨大联系，因为在表达式优化中存在多种特判情况需要处理，导致圈复杂度尤为突出，具体细节在优化策略中分析。
  - Unify的toString方法完成整个表达式的输出，以及SingleFeature(Feature feature, StringBuilder sb)方法完成单个Feature的输出，相关细节在类图分析中的表达式化简与输出部分说明，在处理时较为复杂。
  - Calculate的加法，减法，乘法运算由于需要考虑存在性，遍历是否充分等因素，导致较为复杂。
  当然，由于个人水平有限，在遇到上述复杂情况时，未能充分处理好控制流程，调整判定结构，导致整体复杂度与耦合度较高。
  
  圈复杂度是一种软件度量指标，用于度量程序中的控制流程的复杂性。它是通过计算程序中独立路径的数量来确定的。圈复杂度的值越高，意味着程序的控制流程越复杂，代码的测试和维护难度也越高。
  
  ev(G) 基本复杂度是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。
  
  iv(G) 模块设计复杂度是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。
  
  v(G) 是用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。

二、架构设计体验

1. 程序架构迭代成型

HW_1

难点：从零开始完成代码架构，完成表达式构造，表达式预处理和表达式化简与输出

表达式预处理：参考第一次实验中的架构，完成表达式解析。

首先要除去读入表达式的空白字符，在已知架构基础上增加新的元素，并进行相应处理，当时挺耗时间的。

表达式构造：大致细节参考类图分析的表达式构造部分，区别在于未使用HashSet<Feature>表示多项式，而是使用HashMap<BigInteger,BigInteger>，因为单项式仅有$k*x^m$构成，key为m，value为k，其并不具有充足的可扩展性，这为第二次作业的一次小重构埋下了伏笔。

起初在为用何种容器来存放统一形式思考许久，最终还是选择HashMap<BigInteger,BigInteger>。

表达式化简与输出：大致细节参考类图分析的表达式化简与输出部分，区别在于此处遍历HashMap<BigInteger,BigInteger>，情况较为简单。

化简输出部分参考递归下降直接层次化输出即可，主要还是考虑一些优化，此处参考优化策略

HW_2

难点：加入可嵌套多层括号，自定义函数以及指数函数的要求

可嵌套多层括号：在HW_1中已实现。

自定义函数：大致细节参考类图分析的表达式预处理部分的子过程Function

当时在直接字符串替换还是重复使用类似于Parser的递归下降方法之间犹豫了一下，之后果断选择了前者，因为前者可以直接生成表达式字符串，再重复处理主表达式的处理方式即可。（中间虽然遇到了一些小问题，但是整体感觉还是一个很不错的思路）

指数函数：预处理只要考虑其因子，本架构直接使用Unify进行储存，难点在于如何优化输出，可参考优化策略

当时再优化输出上面花了大功夫，需要考虑很多边界情况，当时是在临近公测提交方才完成并通过评测机评测的，相当惊险！！！（欸，为了性能分）

HW_3

难点：加入求导函数

求导函数：预处理直接处理求导函数返回Unify即可

本次作业的迭代开发相较于HW_2真的柔和很多，之前的架构已经较为完善，并且也没有出现预料的多变量的情况，参考求导的相关法则，直接在Unify中完成求导就好了，亲切多了（\^_\^)

2. 重构说明

正如HW_1中所提及的，当时由于用HashMap<BigInteger,BigInteger>，但其并不具有充足的可扩展性，不能表示$ ka^mexp^{factor}$，后又使用使用类Feature表示$ ka^mexp^{factor}$（单项式），HashSet<Feadture>表示多项式，为此进行了一个小重构

当时因为不知道如何表示$ ka^mexp^{factor}$思考许久，后来想到使用类Feature统一表示，又痛定思痛，没有很困难地完成了小重构（单纯不想重构，觉得自己之前的架构能满足需求，哈哈哈哈）

3. 设计可扩展性

在该架构下，分别由三个部分完成相应的功能，整体架构较为明确，能较为容易完成迭代开发。
充分利用递归下降法以及层次化遍历，完成对表达式的充分解析并能较好满足新元素融入后的调整迭代。

迭代情景 —— 多变量

使用HashMap<String,Feature>的方式存放单项式，用一个类mono存储该容器，再用HashSet<mono>来表示多项式即可，参考上述所陈述的可扩展性，其他部分进行相应的调整即可。

三、程序bug分析

在三次作业的强测与互测当中，均未因正确性判定失分。

起因+解决

起因
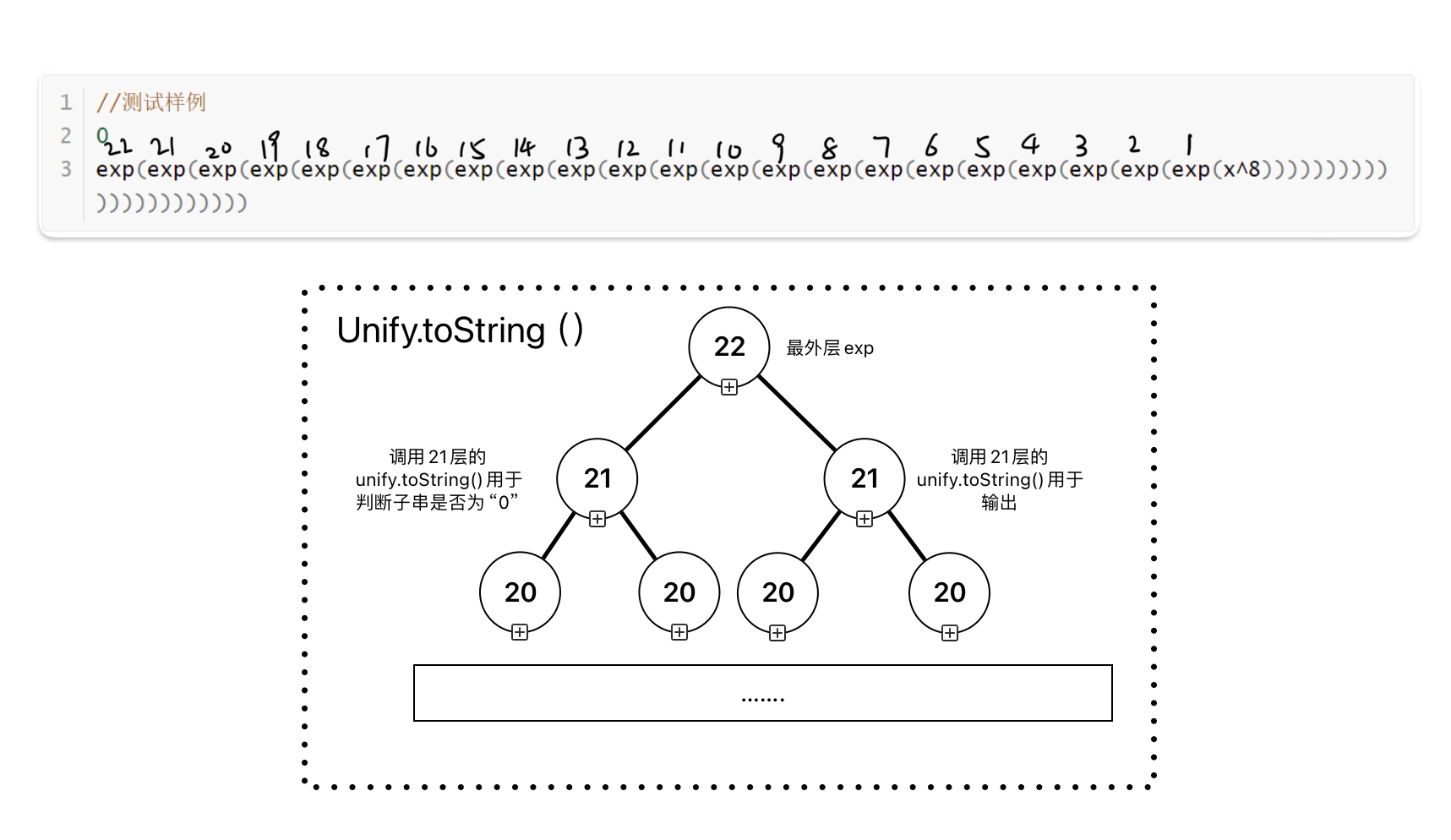
可以说是幸运，在第三次作业的互测中，并没有被hack到，但是在周一晚公布互测结果时，发现自己测试群聊中其他互测房间中的测试样例时，长达十几分钟均未输出结果，从而发现自身代码存在bug，赶忙寻找bug进行修复（虽然没有实际上的意义，但是安心许多……）
1
2
3
//测试样例
0
exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(exp(x^8))))))))))))))))))))))
解决
其中的原因在于这句代码：
1
boolean expno = this.unify.getUnifiedForm().isEmpty() || this.unify.toString() == "0";
该处代码是用来判断指数函数的指数是否为0的，可以细心的发现此处调用了Unify的toString方法，造成如下结果

从而每一层都重复调用Unify.toString()方法，从而造成指数级的复杂度，运行时间暴增！！！

方法复杂度

由于仅将上述代码修改为
1
boolean expno = this.unify.getUnifiedForm().isEmpty();
修复bug前后的复杂度未有明显变化。

四、测试策略

评测机搭建

前言：

在室友的帮助下，并借助于ChatGPT，完成数据生成器的搭建，并借助于python的第三方库，对自己代码的输出结果进行检测，从而输出评测结果。

过程：

在评测时，利用上述数据生成器，生成测试样例，再将自己代码的输出结果与互测房中的其他同学的输出结果对扣（此处检测器是在自己原有代码的基础上修改的，将两个输出表达式相减判断是否为“0”即可），从而判断是否正确（当然是对自己代码的充分自信，哈哈哈！）

结果：

使用上述方法，成功hack别人两此，均为第二次作业
1
2
3
4
//测试样例_1
1
h(z,y)=-exp((-y)^0)
-exp(h(76,x^2))
1
2
//标准输出_1
-exp(-exp(1))
由上述可见，其未在-exp(1)外添加括号，导致评测结果Your answer has format error.
1
2
3
4
//测试样例_2
1
f(x)=-2
exp((x*f(x)*+2-+x^2*-3)^2)
1
2
//标准输出_2
exp((16*x^2+48*x^3+9*x^4))
未处理好exp内因子的化简问题，导致评测结果Wrong Answer |

依托形式化表达构造特定数据

每个对象都要出现

每种组合规则都要出现

每种符号模式都要出现

每种系数模式都要出现

输入的组合

具有明确的pattern和组合性

表示结构：线性序列结构

逻辑结构：带递归的层次结构

五、优化策略

表达式

若无系数为正的Feature，直接输出

若存在系数为正的Feature，任选其一优先输出

Feature由数字、幂函数、指数函数组成，逐一分类讨论即可

数字

去除前导0

若为正数，省略+

若为负数，输出+

幂函数

指数为1，输出x

指数不为1，输出x^index

指数函数

对指数函数的指数因子进行优化，提取最大公因数gcd

保证最大公因数为正（指数为非负整数）

提取后保证输出结果格式正确

exp((2*x)) -> exp(x)^2：此处可以去括号优化

exp((-2*x)) -> exp((-x))^2：此处不能去括号优化

exp(factor)的factor若为表达式因子一定要加上括号

提取最大公因式前的指数函数长度可能小于提取后的长度，需进行比较选择较小值

exp((51*x+33*x)) -> exp((17*x+11*x))^2：此处提取前长度小于提取后长度，不需提取最大公因数

提取最大公因数可能并不是并不是最优化的结果

优化目标：exp((132*x+36*x))

优化结果一：exp((11*x+3*x))^12

优化结果二：exp((33*x+9*x))^4

由上可见，前者的优化结果不如后者的优化结果

需保证最大公因数大于等于2方可进行检验提取

我将Feature分成下面六类，接下来进行逐一分析。

1
2
3

public enum Type{
    Num, Variable, Exp, NumExp, NumVari, VariExp, NumVariExp
}

	`Num`	`Vari`	`Exp`	`NumExp`	`NumVari`	`VariExp`	`NumVariExp`
系数是否为1	✖	✔	✔	✖	✖	✔	✖
幂函数指数是否为0	✔	✖	✔	✔	✖	✖	✖
指数函数指数为0	✔	✔	✖	✖	✔	✖	✖
输出	数字	幂函数	指数函数	数字*指数函数	数字*幂函数	幂函数*指数函数	数字指数函数\幂函数

六、心得体会

第一次作业的时候，比较担心自己刚开学的状态不佳（刚过完年，嘻嘻），害怕不能完成作业，但从自己刚开始学习递归下降法，逐渐理解文法解析，到将第一次实验应用到自己的程序架构实现当中，慢慢解决代码编写中的问题时，开始重拾信心。

第二次作业确定了字符串解析，优化策略后，之后就是落地实现的过程，编写代码，到反复测试，感觉很充实，很享受自己代码逐渐完善的过程。

第三次作业给人感触不深，主要是互测后发现了bug（在程序bug分析中已提及），开始汗流浃背，庆幸我的互测房的“柔和风气”，最后经过仔细寻找，方才从几百行代码中揪出罪魁祸首（诶，就一句代码导致的……）

完成这篇博客的过程正是回顾这一个单元的过程，重新理解和分析一个月以来的成果，对面向对象有了新的认识，既为自己的努力感到自豪，也期待下一单元的磨炼！！！

在本次单元中，整体来说是一个很舒畅，很充实的经历，不断学习，深入认识。

七、未来方向

建议将类的内聚和相互间的耦合情况的评测指标加入整个代码评测要求当中，便于学生在进行代码架构时着重考虑圈复杂度，ev(G)，iv(G)，v(G)，降低代码的测试和维护难度，提高代码质量（本次作业我出现了上述问题，最后完成整个单元的学习后，发现最终代码架构的圈复杂度超于常值，未处理好类的内聚以及相互的耦合关系）

一、 程序架构分析

1. 类图分析

最终架构总UML图

表达式化简与输出部分

表达式构造部分

表达式预处理部分

优缺点分析

2. 度量分析

代码规模

类复杂度

表达式构造部分

表达式预处理部分

表达式化简与输出部分

二、 架构设计体验

1. 程序架构迭代成型

HW_1

HW_2

HW_3

2. 重构说明

3. 设计可扩展性

三、 程序bug分析

起因+解决

起因

解决

方法复杂度

四、 测试策略

评测机搭建

依托形式化表达构造特定数据

输入的组合

五、 优化策略

表达式

数字

幂函数